6 Stochastic population growth

6.1 Background

In contrast to the deterministic nature of the geometric growth model, a stochastic version of the model introduces an element of randomness, making it more reflective of real-world scenarios. Instead of assuming fixed and predictable growth rates, the stochastic model incorporates uncertainties and fluctuations that occur due to various factors, such as environmental variability, chance events, and individual-level variations in reproductive success. By embracing this stochastic approach, the population dynamics become more realistic, allowing us to better understand and predict the inherent variability and uncertainties associated with natural populations. This stochastic framework provides a valuable tool for ecologists and researchers to explore the dynamics of real populations under more complex and dynamic conditions.

Remember: this model still allows for unbounded population growth (the populations are not influenced by population density).

We’ll focus on the discrete (Geometric) growth model: $N_{t+1}=\lambda N_t$.

Because $\lambda = \mathrm{e}^{r_m}$ (and $r_m = \ln(\lambda)$; see the notation box in the Part 2 introduction), we can rearrange the equation to express it as $N_{t+1}=\mathrm{e}^{r_m} N_t$.

Therefore, we can predict next year’s population size from this year’s population if we know either $r_m$ or $\lambda$.

We will create some models in Excel, and then in R, to explore the effect of stochastic variation in the population growth rate.

We can simulate variation in $r_m$ by drawing a random number from a normal distribution with a particular mean ($\bar{r_m}$) and variance ($\sigma_{r_m}^2$) (Fig. 6.1). The $\bar{r_m}$ value determines the long-term average while the $\sigma_{r_m}^2$ estimates how much “spread” there is in the data from year to year.

The figure shows 1,000 values drawn from a normal distribution with mean 0.05 and variance 0.1 (the settings you will use in this practical). The peak of the $r_m$ distribution is just above 0 (at 0.05), so on average the population will tend to grow. However, in poor years $r_m$ is $<$ 0, so the population will decline in those years. With this much variation, declines are almost as common as increases: about 44% of years have $r_m < 0$. Both the mean value and the spread of the distribution (i.e. variance) determine the fate of the population.

Remember that we can convert $r_m$ to $\lambda$ by taking the exponential, because $r_m = \ln(\lambda)$.

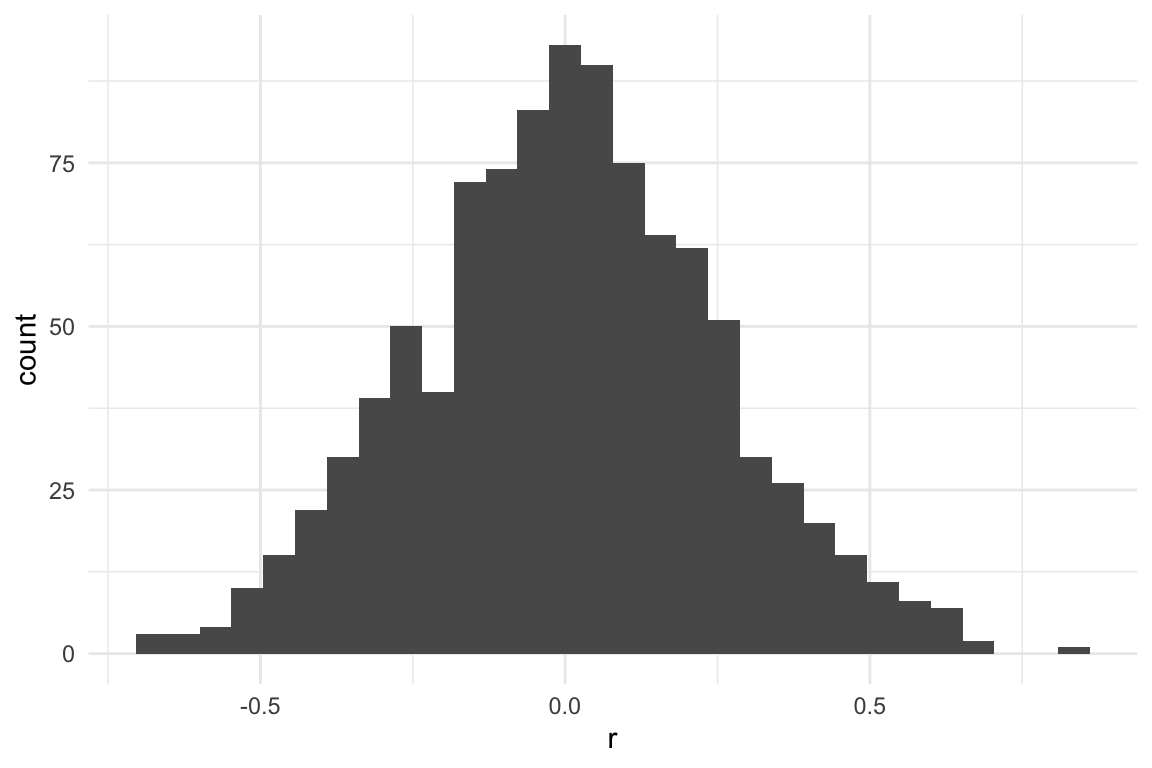
Figure 6.1: 1,000 values of $r_m$ drawn from a normal distribution with mean 0.05 and variance 0.1. The dashed line marks $r_m = 0$.

When using the equation above to calculate population at time $t+1$ ($N_{t+1}$) from the population at time $t$ ($N_t$), one would draw a random $r_m$ value from this distribution. Sometimes $r_m$ will be high, other times it will be low, most of the time it will be from around the middle of the distribution.

Average growth: why the mean $\lambda$ is misleading

In this model $r_m = \ln \lambda$ is drawn afresh each year. After $t$ years, $\ln N_t$ is $\ln N_0$ plus the sum of $t$ random $r_m$ values, so the median (typical) trajectory grows at exactly the mean, $\bar{r}_m$, per year: $\lambda = e^{0.05} = 1.051$ with our settings. The arithmetic mean of $\lambda$ is larger, $e^{\bar{r}_m + \sigma^2/2} = e^{0.05 + 0.05} = 1.105$, because a few very good years pull the average up. A population projected with the average $\lambda$ would therefore grow about twice as fast (on the log scale) as a typical stochastic population. Long-run growth follows the geometric mean of $\lambda$ ($e^{\bar{r}_m}$), not the arithmetic mean. Put the other way round: if the arithmetic mean $\lambda$ stays the same, more year-to-year variation lowers long-run growth.

You may meet the rule that extinction is (eventually) almost certain when $\sigma^2 > 2\bar{r}$. That rule takes $\bar{r}$ as the average growth rate on the $\lambda$ scale, so its long-run growth is $\bar{r} - \sigma^2/2$. In this practical $r_m$ is drawn on the log scale, so long-run growth is $\bar{r}_m$ itself, and the population is doomed in the long run only if $\bar{r}_m \leq 0$. Both say the same thing: a population is doomed if its long-run (geometric-mean) growth rate is zero or below. The rule is also about the very long run; over 50 generations, extinction risk can be well below 1.

Learning outcomes:

Increased competence in using Excel formulae for mathematical modelling.
Understanding the concept of stochasticity in simple population models.
Competence in using mathematical models in Excel to strengthen own understanding of biological processes.
Understanding how stochasticity relates to (i) uncertainty in the prediction of population trajectories and (ii) probability of (local) extinction.

6.2 Worked example

6.2.1 Inputs

Population this year: $N_t = 100$
$r_m$ drawn at random for this year: $-0.2$ (a poor year)

6.2.2 Steps

Convert $r_m$ to $\lambda$: $\lambda = e^{-0.2} = 0.819$.
Project one year: $N_{t+1} = 100 \times e^{-0.2} = 81.9$.

6.2.3 Output and interpretation

$N_{t+1} = 81.9$: in this poor year the population shrinks by about 18%. Next year a new $r_m$ is drawn (for example $+0.3$, giving $81.9 \times e^{0.3} = 110.5$), and so on. Repeating this step with a fresh random $r_m$ each year produces one stochastic trajectory.

6.3 Your task

Use the Excel worksheet, StochasticPopulationGrowth.xlsx, to study how stochastic population growth works with this simple model.

In this practical we use the same settings throughout: $r_m$ is drawn from a normal distribution with mean 0.05 and variance 0.1. Years of growth then only slightly outnumber years of decline (about 56:44). This means a population can grow on average yet still crash by chance, especially when starting size is small.

In the Excel template, first set the mean of $r_m$ to 0.05 and the variance to 0.1 (the template may contain other values), and use a starting population of 100.

Use Excel formulae to calculate deterministic population size through time (25 generations, t = 0 to 25, with starting population of 100), using the multiplication rate for the mean $r_m$, $\lambda = e^{\bar{r}_m}$.
Use charts to plot the results. (you already did this last time!)
Use a formula to generate a column of stochastic $r_m$ values, based on a chosen mean and variance. The formula refers to the cells that hold the mean and the variance of $r_m$; check where these are in your sheet (in the template they are G10 and G11). In English versions of Excel the function may be written either as =NORM.INV(RAND(), $G$10, SQRT($G$11)) (newer versions) or =NORMINV(RAND(), $G$10, SQRT($G$11)) (older versions), while in Danish Excel it appears as =NORMINV(SLUMP(); $G$10; KVROD($G$11)). If you encounter errors, check whether your copy of Excel expects commas or semi-colons as argument separators and adjust the formula accordingly.
Use the same procedure as before, to create a stochastic population size vector (stochastic N). Remember to convert $r_m$ to $\lambda$ by taking the exponential (=EXP(...); Danish Excel: =EKSP(...)).
Compare the two trajectories using a chart.
Try altering initial population size, mean population growth, and the amount of stochasticity (Variance).
In this model N is multiplied by $e^{r_m}$, which is always positive, so N can never reach exactly 0. Instead, we treat the population as (quasi-)extinct if N falls below 1 at any point, i.e. fewer than one individual is left (the R code below uses the same rule). What happens to extinction risk as stochasticity (variance) increases? What happens when initial N is small? Does the population ALWAYS survive if the mean population growth rate, $\bar{r_m}$, is $>$ 0?

Note: Excel re-randomises the random numbers every time you change any cell in the sheet. This is OK, and allows you to explore a stochastic simulation many times.

6.4 Simulations in R

Excel is of limited use to really get a feel for this. For the next part we’ll use R.

The simulation below repeats the stochastic projection many times, so you can estimate extinction risk and see how it is related to starting population size, mean growth rate, and the amount of stochasticity.

You can copy/paste the code below into R.

The output of the modelling is shown in Fig. 6.2

Copy-and-paste the code below into a text file (or directly into R).

The final line of the code (nExtinct/nTrials) gives you an estimate of extinction probability - the proportion of trials in which the population falls to 1 or fewer individuals at some point, the same rule as in the Excel exercise. The R settings use the same mean (0.05) and variance (0.1) of $r_m$ as the Excel exercise, but a smaller starting population (10), so that extinctions are common enough to see.

Modify the simulation settings to explore what happens to (i) the plot of population growth and (ii) extinction risk, when you vary mean.r ($\bar{r_m}$), the amount of stochasticity ($\sigma_{r_m}^2$) (var.r), and the number of generations (nGen).

#Simulating stochastic geometric population growth rate

#Simulation settings (try changing these)
mean.r = 0.05 # the mean value of r_m
var.r = 0.1 # the variance in r_m (stochasticity)
startPop = 10 # pop size at start
nGen = 50 # number of generations
nTrials = 1000 # number of repeated simulations

##########################################################
#If you are unfamiliar with R, don't edit below this line!
##########################################################

pseudoExtinction = 1

# First randomly generate some r values
rValues <- matrix(rnorm(nTrials * nGen, 
                        mean = mean.r, 
                        sd = sqrt(var.r)),
                  ncol = nTrials,
                  nrow = nGen)

# Use a histogram to see what they look like 
# (uncomment the line below)
# hist(rValues,col="grey",main="")

# Now run the simulations to see what the resulting 
#population growth looks like
trials = matrix(data = NA, nrow = nGen, ncol = nTrials)
for (j in 1:nTrials) {
  popSize = startPop
  for (i in 2:nGen) {
    stoch.r = rValues[i, j]
    newN = popSize[i - 1] * exp(stoch.r)
    # once the population falls below the threshold it is extinct,
    # so set it to 0 (it cannot recover)
    if (newN < pseudoExtinction) newN = 0
    popSize = append(popSize, newN)
  }
  trials[, j] = popSize
  rm(popSize)
}

#Calculate probability of (pseudo)extinction
minvals <- apply(trials, 2, min)
nExtinct <- length(minvals[minvals <= pseudoExtinction])
probExtinct <- nExtinct / nTrials
cat("Pseudo-extinction probability:", round(probExtinct, 3), "\n")

## Pseudo-extinction probability: 0.058

6.4.1 Example stochastic trajectories

#Make a plot of the population trajectories
yMax <- max(100000, max(trials)) # upper limit of the y-axis
plot(
  1:nGen,
  log(seq(0.1, max(trials), length.out = nGen)),
  type = "n",
  axes = F,
  xlab = "Time",
  ylab = "log(N)",
  ylim = log(c(0.1, yMax))
)
matlines(log(trials[, 1:min(100, nTrials)]), # plot up to 100 trajectories
         col = "#FF234520",
         lty = 1,
         lwd = 3)
axis(1)
axis(2,
     at = log(10^(-1:ceiling(log10(yMax)))),
     labels = 10^(-1:ceiling(log10(yMax))))
abline(h = log(pseudoExtinction), lty = 2)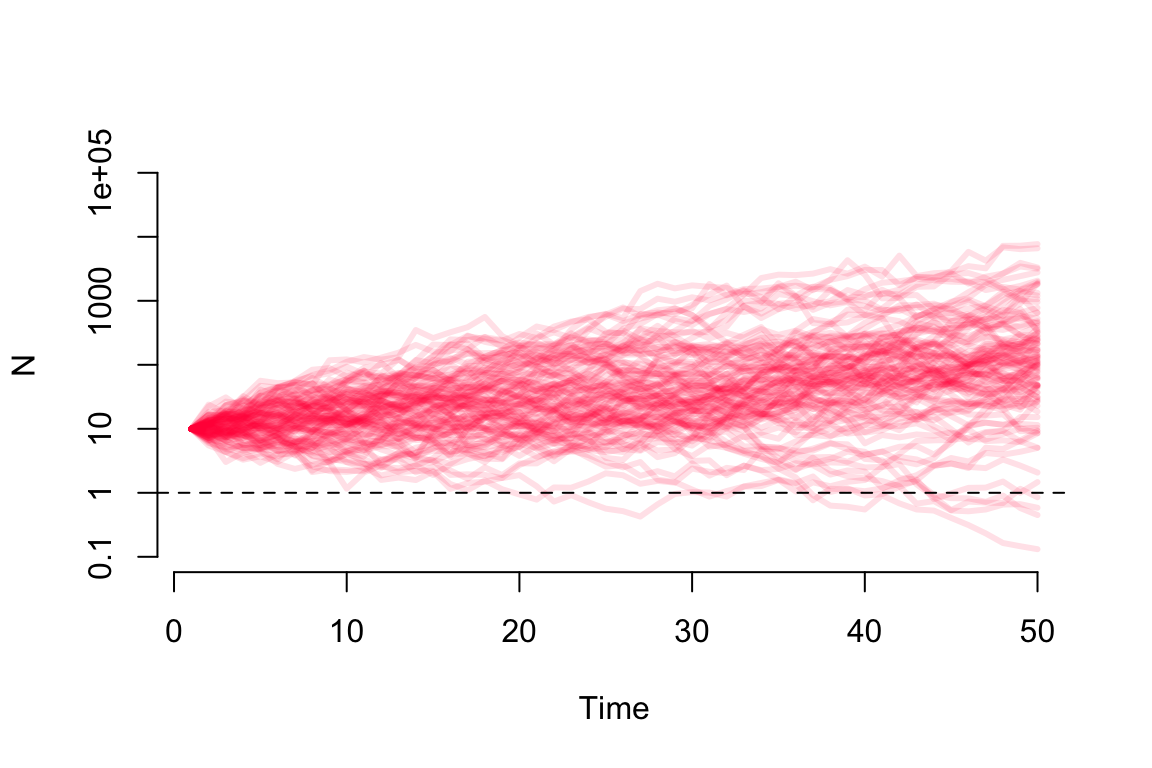

Figure 6.2: An example of stochastic population projection (100 of the 1,000 simulations, 50 generations)

6.5 Things to try

Work through these experiments and note what happens to (a) the plot and (b) the extinction probability each time.

Run the code as-is. Note the extinction probability and the spread of trajectories.
Keep mean.r = 0.05 but increase var.r to 0.5. How does extinction risk change?
Reset var.r = 0.1, then reduce startPop from 10 to 3. Does starting population size matter?
Set mean.r = 0.0 (population neither growing nor shrinking on average). Is extinction certain, unlikely, or somewhere in between?
Challenge: find a combination of mean.r and var.r where mean.r > 0 but extinction probability exceeds 0.5. What does this tell you?

6.6 Questions

What is the main difference between deterministic and stochastic population growth models?
Describe how incorporating randomness into the stochastic model makes it more realistic for understanding real-world populations.
Simulate a scenario where two populations with identical growth rates experience different outcomes due to stochastic factors. Explain the implications of these findings.
What can this stochastic model tell us about extinction risk and population size?
What can this stochastic model tell us about extinction risk and environmental variation?

6.7 Takeaways

Stochasticity introduces variability in trajectories.
Long-run growth follows the mean of $r_m$ (the geometric mean of $\lambda$), not the arithmetic mean of $\lambda$, so projecting with the average $\lambda$ overestimates typical growth.
Even when the average growth rate is positive, stochastic variation can create a real risk of extinction.
Small populations are more vulnerable to random declines and extinction.
The variance of $r_m$ can be as important as its mean for long-term population persistence. This is why conservationists worry about increasing environmental variability, not just declining average conditions.
Running a model many times (as in the R simulation) reveals the distribution of possible outcomes, a much richer picture than any single trajectory provides.