24 Discrete-time Lotka-Volterra Predator-Prey Model in R

Learning outcomes:

  • Implement and explore a discrete-time predator-prey model in R.
  • Understand how time steps introduce delays and affect stability.
  • Compare discrete-time dynamics to continuous-time dynamics.

24.1 Key idea

With \(\Delta t = 1\), the phase plane typically shows expanding spirals, reflecting instability introduced by discrete time steps.

24.2 Introduction

The Lotka-Volterra model describes the interaction between predators and prey. This document demonstrates how to program the discrete-time version of the model in R, explore its features, and visualise the dynamics of predator and prey populations over time. The time step (\(\Delta t\)) can be adjusted to explore the impact of a time delay in the system. In ecological systems, time delays can represent biological processes such as the time it takes for predators to respond to changes in prey density, for prey populations to recover after predation. If \(\Delta t\) is set to 1, this model is equivalent to a year-by-year model (as we have fitted in Excel in class), where the impact of predators on prey has a 1 year lag. i.e. the growth of predators, depends on the availability of prey 1 year ago and the growth of prey depends on the amount of predators 1 year ago.

There are two ways to think about \(\Delta t\). With \(\Delta t = 1\) this is a model of populations that really do change in steps (e.g. one breeding season per year). With \(\Delta t\) very small, nothing biological has changed: we are simply calculating the continuous-time model more accurately, in many small steps. The parameters and the starting numbers are the same as in the Excel spreadsheet and the continuous-time R chapter.

24.3 Step 1: Define the Model

The discrete-time equations are as follows:

  • Victim (prey) population growth:
    \(V_{t+1} = V_t + \Delta t \cdot (R \cdot V_t - a \cdot C_t \cdot V_t)\)

  • Consumer (predator) population growth:
    \(C_{t+1} = C_t + \Delta t \cdot (a \cdot f \cdot V_t \cdot C_t - q \cdot C_t)\)

Note that, when \(\Delta t = 1\), the model is as follows:

  • Victim (prey) population growth:
    \(V_{t+1} = V_t + R \cdot V_t - a \cdot C_t \cdot V_t\)

  • Consumer (predator) population growth:
    \(C_{t+1} = C_t + a \cdot f \cdot V_t \cdot C_t - q \cdot C_t\)

Compare these to Equations 1 and 2 in the Excel exercise PDF.

The function below implements these equations in R.

discrete_predator_prey_model <- function(time_steps, dt, initial_state, parameters) {
  # Initialise vectors to store populations
  time_steps <- round(time_steps)
  V <- numeric(time_steps + 1)
  C <- numeric(time_steps + 1)
  time <- seq(0, time_steps * dt, by = dt)
  
  # Set initial populations
  V[1] <- initial_state["V"]
  C[1] <- initial_state["C"]
  
  # Extract parameters
  R <- parameters["R"]
  a <- parameters["a"]
  f <- parameters["f"]
  q <- parameters["q"]
  
  # Loop through time steps to calculate populations
  for (t in 1:time_steps) {
    # max(0, ...) stops populations going negative (like IF() in Excel)
    V[t + 1] <- max(0, V[t] + dt * (R * V[t] - a * V[t] * C[t]))
    C[t + 1] <- max(0, C[t] + dt * (a * f * V[t] * C[t] - q * C[t]))
  }
  
  # Combine results into a data frame
  data.frame(time = time, V = V, C = C)
}

24.4 Step 2: Set Parameters and Initial Conditions

We set the parameters, initial conditions, the total time to simulate (total_time) and the time step (\(\Delta t\)). The number of steps is calculated from these, so that changing \(\Delta t\) always covers the same total time and the runs can be compared fairly.

parameters <- c(R = 0.25,  # Victim (prey) growth rate
                a = 0.01,  # Attack rate
                f = 0.008, # Conversion efficiency
                q = 0.1)   # Consumer (predator) death rate

initial_state <- c(V = 1000,  # Initial victim population
                   C = 20)    # Initial consumer population

total_time <- 300             # Total time to simulate
dt <- 1                       # Time step (dt), 1 = a standard discrete model
time_steps <- total_time / dt # Number of time steps needed to cover total_time

24.5 Step 3: Simulate the Model

We simulate the model for the specified parameters and time steps.

output_df <- discrete_predator_prey_model(time_steps = time_steps, dt = dt, 
                                          initial_state = initial_state, 
                                          parameters = parameters)

24.6 Step 4: Visualise the Dynamics

24.6.1 Population Dynamics Over Time

The plot below shows the changes in consumer and victim populations over time.

# Make room in the right-hand margin for the second axis label
par(mar = c(5, 4, 4, 5))

# Plot victim population on the primary y-axis
plot(output_df$time, output_df$V, type = "l", col = "blue", lwd = 2, 
     ylab = "Victim Population (V)", xlab = "Time", main = "Discrete Predator-Prey Dynamics")

# Add consumer population on a secondary y-axis
par(new = TRUE)
plot(output_df$time, output_df$C, type = "l", col = "red", lwd = 2, 
     axes = FALSE, xlab = "", ylab = "")
axis(side = 4, col = "red", col.axis = "red")
mtext("Consumer Population (C)", side = 4, line = 3, col = "red")

# Add legend
legend("topright", legend = c("Victim (V)", "Consumer (C)"), 
       col = c("blue", "red"), lwd = 2)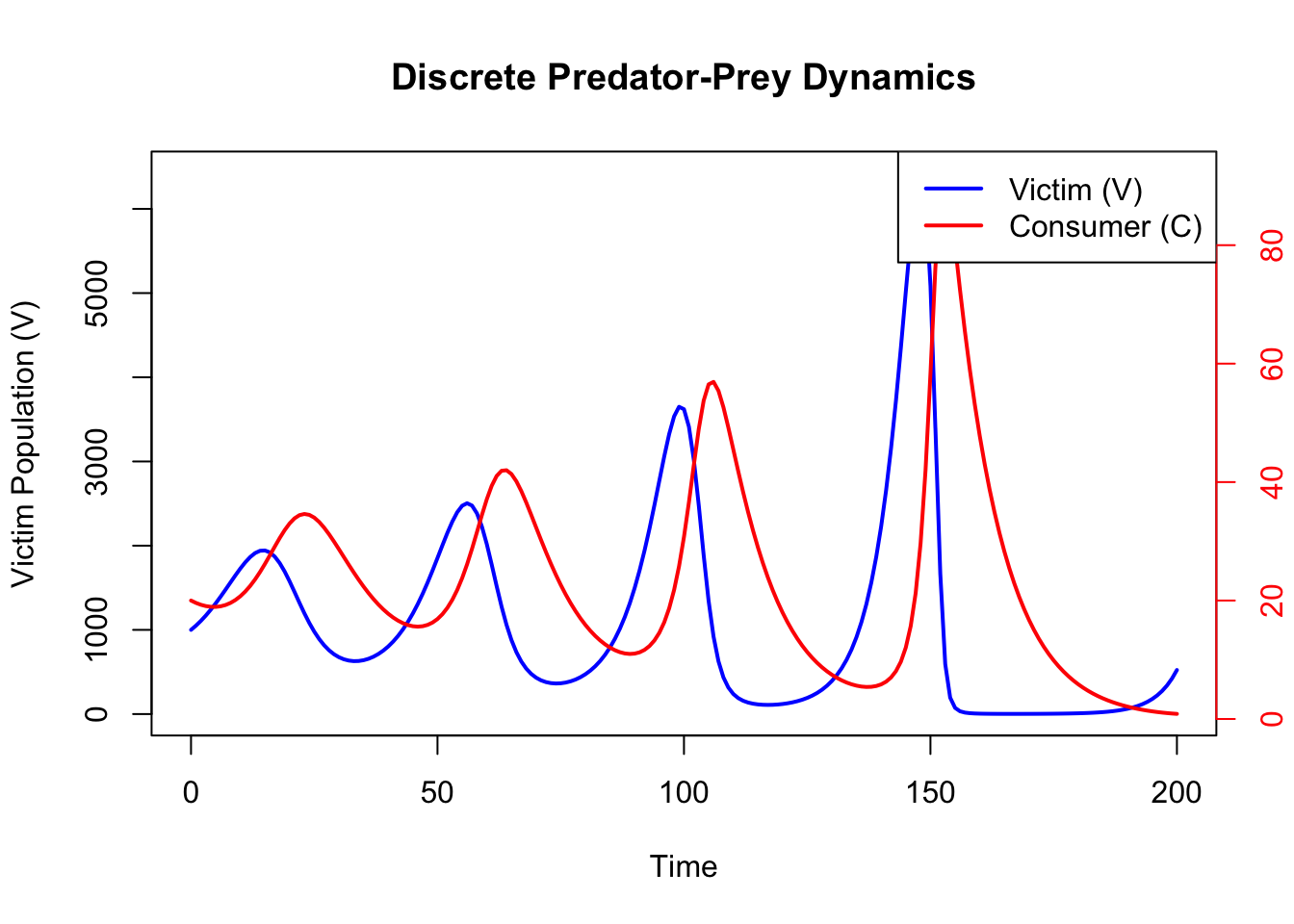

24.6.2 Phase Plot with ZNGIs

The phase plot shows the relationship between victim and consumer populations.

### Phase Plot with ZNGIs, Initial Point, and Arrow
plot(output_df$V, 
     output_df$C, 
     type = "l", 
     col = "purple", 
     lwd = 2, 
     xlab = "Victim (V)", ylab = "Consumer (C)", 
     main = "Discrete Predator-Prey Dynamics with ZNGIs")

# Add Consumer ZNGI: no change in C when V = q / (a * f) (a vertical line)
abline(v = parameters["q"] / (parameters["a"] * parameters["f"]),
       col = "red", lwd = 2, lty = 2)

# Add Victim ZNGI: no change in V when C = R / a (a horizontal line)
abline(h = parameters["R"] / parameters["a"], col = "blue", lwd = 2, lty = 2)

# Add point for initial population sizes
points(output_df$V[1], output_df$C[1], pch = 19, col = "black", cex = 1.5)

# Add a direction arrow only if the final step has visible movement.
n <- nrow(output_df)
step_inches <- c(
  diff(grconvertX(output_df$V[c(n - 1, n)], from = "user", to = "inches")),
  diff(grconvertY(output_df$C[c(n - 1, n)], from = "user", to = "inches"))
)
if (all(is.finite(step_inches)) && sqrt(sum(step_inches^2)) > 1e-3) {
  arrows(x0 = output_df$V[n - 1], y0 = output_df$C[n - 1],
         x1 = output_df$V[n], y1 = output_df$C[n],
         col = "purple", length = 0.1, lwd = 2)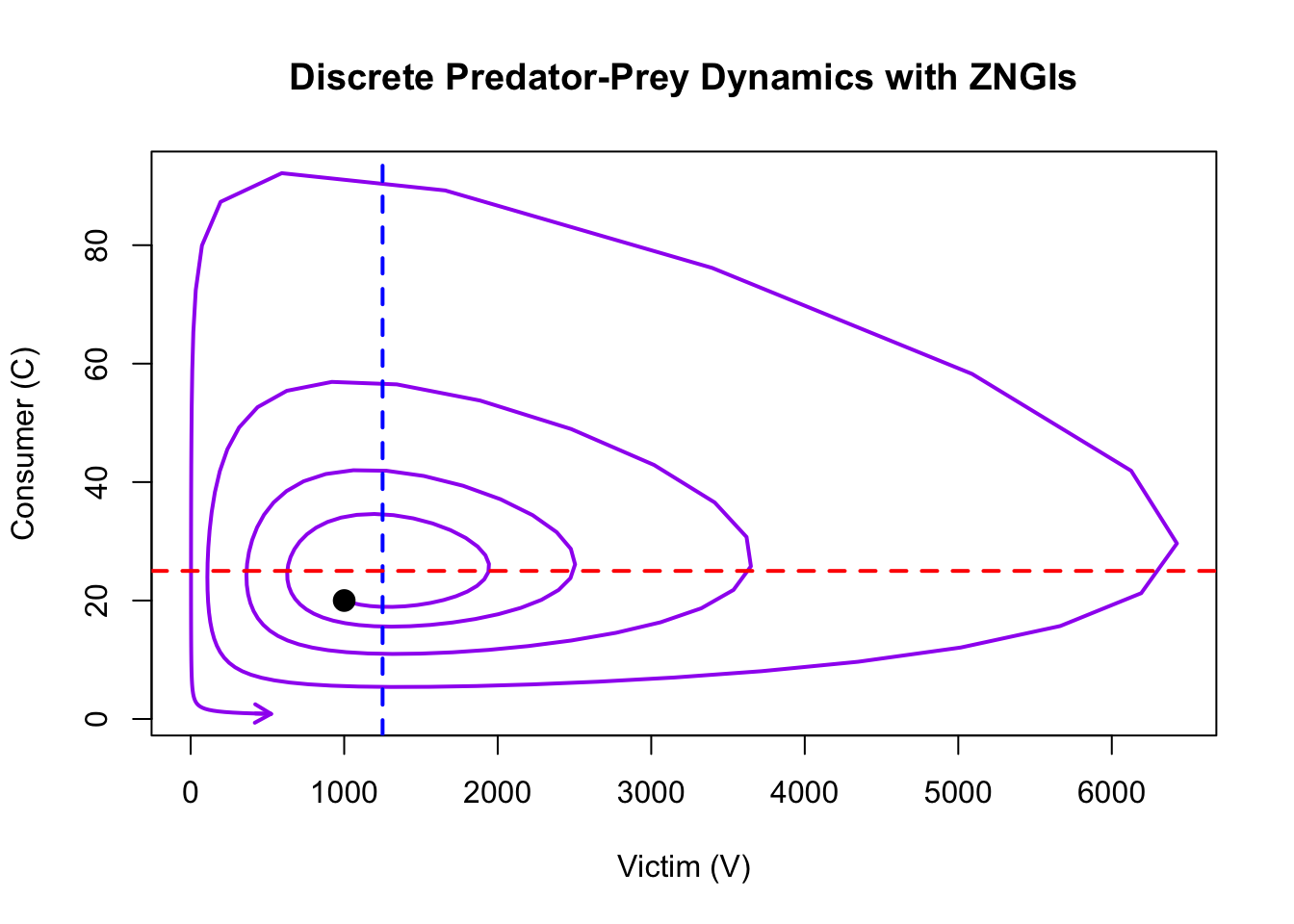
}

24.7 Your task

Before each run, predict what you will see (sketch the phase plot), then check.

  • Run the model with the default settings (\(\Delta t = 1\), total_time = 300). How does the phase plot differ from the closed orbit in the continuous-time chapter? When does the first population hit zero? Find it with output_df$time[which(output_df$C == 0 | output_df$V == 0)[1]].
  • Decrease \(\Delta t\) to 0.1 (keep total_time = 300; the number of steps is recalculated for you, so re-run the parameter chunk as well as the simulation) and compare the phase plane behaviour to \(\Delta t = 1\). Then try \(\Delta t = 0.01\).
  • Increase \(\Delta t\) to 2 and observe whether extinction happens faster.
  • Change \(R\) or \(q\) (e.g. double one of them) with \(\Delta t = 1\). Does the spiral grow faster or slower? Now double \(a\) or \(f\) instead. Which parameters control how quickly the spiral grows? (Careful: changing \(a\) or \(f\) also moves the equilibrium, so the default start is then nearer to or further from it. Compare how fast the spiral widens, not only when it ends.)

24.8 Conclusion

This document demonstrates how to implement and explore the discrete-time Lotka-Volterra predator-prey model. By adjusting the time step (\(\Delta t\)) and other parameters, you can investigate how predator-prey dynamics are influenced by ecological factors. With the default settings (\(\Delta t = 1\)), the time lag of one step makes the phase plot spiral outwards: the cycles grow until the prey are wiped out (they hit zero at \(t = 220\)), after which the predators starve and dwindle towards zero. Smaller time steps make the spiral grow more slowly, and with \(\Delta t = 0.01\) the orbit is almost closed, like the continuous-time model. Larger time steps make it grow faster: with \(\Delta t = 2\) the prey hit zero at \(t = 142\). Contrast this with the perpetual (neutrally stable) oscillations you get with the continuous-time model.

24.9 Takeaways

  • Discrete time steps destabilise the predator-prey cycles of the continuous-time model: the populations react one step too late, so each cycle overshoots a little more than the last.
  • Each time step, the distance from the equilibrium grows by a factor of about \(\sqrt{1 + \Delta t^2 R q}\). This depends on the prey growth rate, the predator death rate and the step length, but not on the attack rate or conversion efficiency. With the default values it is about 1.012 per step (roughly 1 % per step).
  • Smaller \(\Delta t\) values bring the discrete model closer to the continuous-time behaviour.