Age-from-stage analyses

Introduction

Regardless of whether the stage classes of a matrix population model (MPM) are based on age, size, and/or ontogeny, it’s possible to obtain age-specific schedules of survivorship (lx) and reproduction (mx) using ‘age-from-stage’ methods, as described by Caswell (2001).

Preliminaries

We’ll start by loading a few packages and a dataset that we’ll be using throughout this vignette.

library(Rage) # load Rage
data(mpm1) # load data object 'mpm1'
mpm1 # display the contents
#> $matU
#>         seed small medium large dormant
#> seed    0.10  0.00   0.00  0.00    0.00
#> small   0.05  0.12   0.10  0.00    0.00
#> medium  0.00  0.35   0.12  0.23    0.12
#> large   0.00  0.03   0.28  0.52    0.10
#> dormant 0.00  0.00   0.16  0.11    0.17
#> 
#> $matF
#>         seed small medium large dormant
#> seed       0     0   17.9  45.6       0
#> small      0     0    0.0   0.0       0
#> medium     0     0    0.0   0.0       0
#> large      0     0    0.0   0.0       0
#> dormant    0     0    0.0   0.0       0

Age-from-stage methods with a single matrix population model

This MPM has 5 stage class, and it’s apparent from the dimnames attribute that the stages are not based solely on age. Nonetheless, we can estimate age-schedules of survivorship and reproduction using the functions mpm_to_lx() and mpm_to_mx() from Rage.

dimnames(mpm1$matU)
#> [[1]]
#> [1] "seed"    "small"   "medium"  "large"   "dormant"
#> 
#> [[2]]
#> [1] "seed"    "small"   "medium"  "large"   "dormant"

# extract U and F matrices
mat_U <- mpm1$matU
mat_F <- mpm1$matF

# calculate lx
lx <- mpm_to_lx(mat_U, start = 1, xmax = 30)

# calculate mx
mx <- mpm_to_mx(mat_U, mat_F, start = 1, xmax = 30)

In addition to the relevant matrix components, the mpm_to_* functions require two extra arguments. The first, start, is an integer indicating which stage reflects the ‘start of life’. Usually this will be 1, but sometimes we might want to skip over stages that are propagule (i.e. seed) or dormant. The MPM we selected begins with a seed stage, so we may want to start from the second stage, corresponding to start = 2. The second argument, N is the number of time steps to calculate over.

# calculate lx
lx <- mpm_to_lx(mat_U, start = 1, xmax = 30)

# calculate mx
mx <- mpm_to_mx(mat_U, mat_F, start = 1, xmax = 30)

Let’s take a look at the trajectories.

plot(lx, ylim = c(0, 1), type = "l", xlab = "Age")

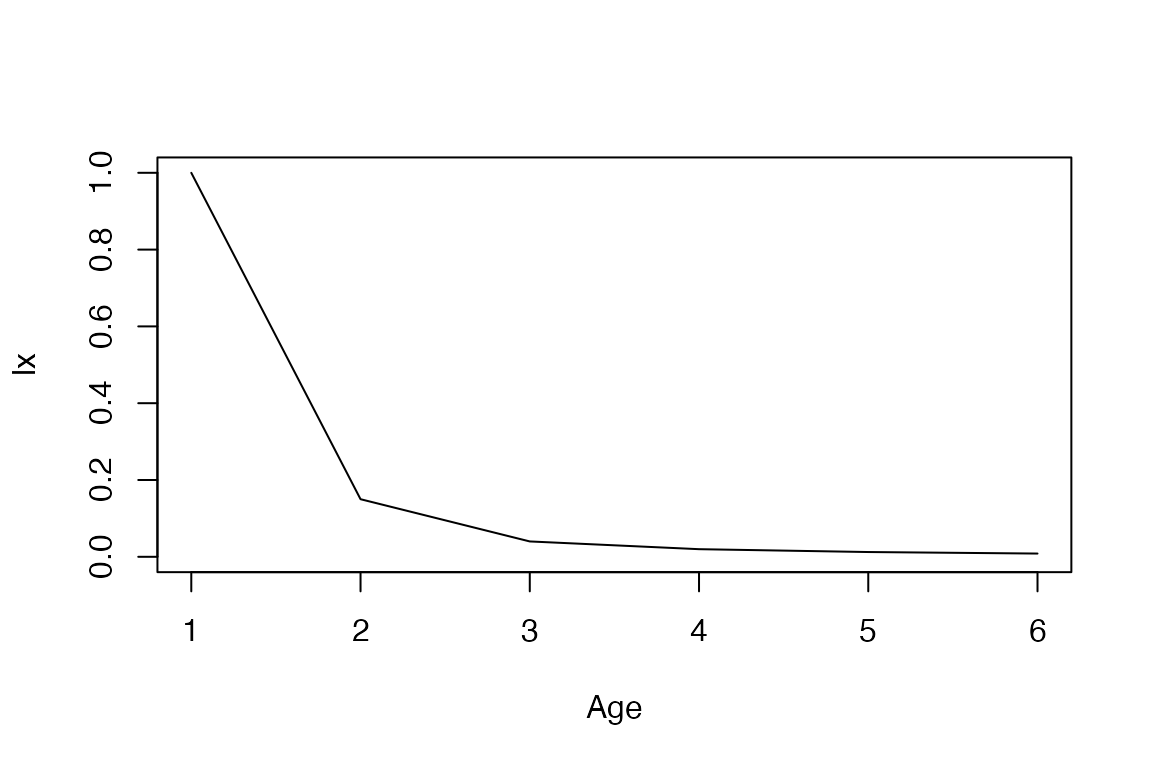
plot(mx, type = "l", xlab = "Age")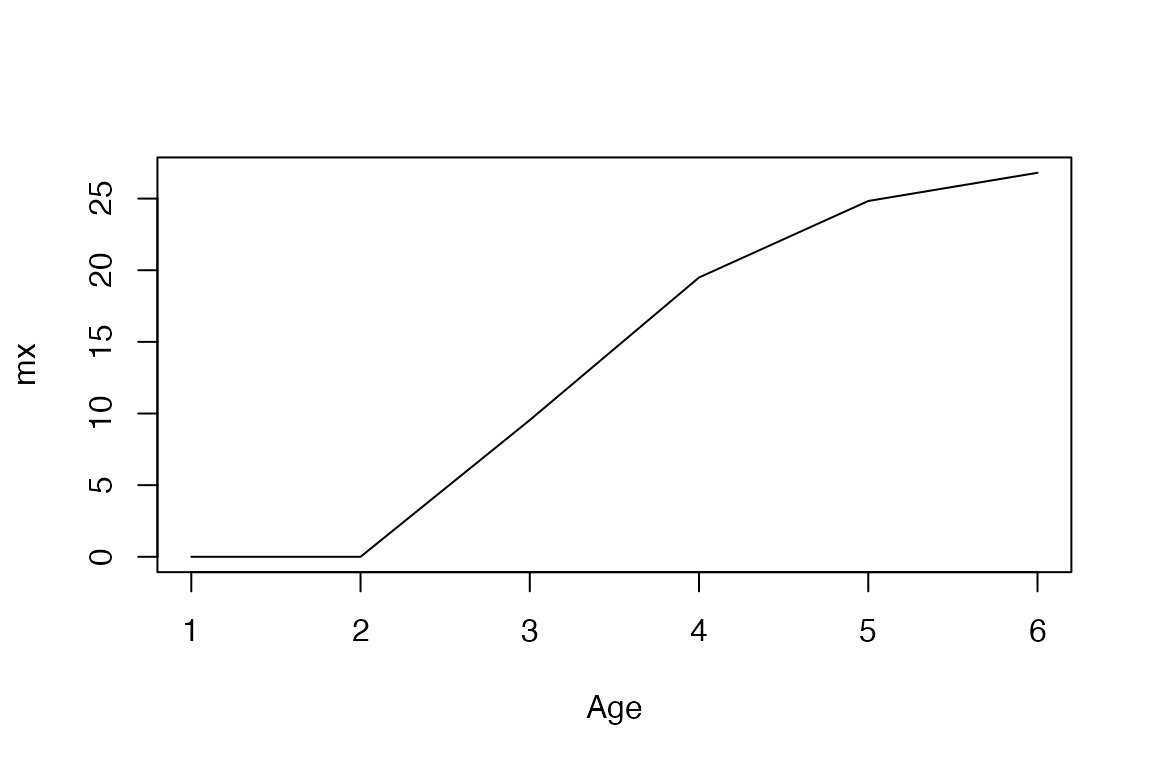

Extending to many matrix population models

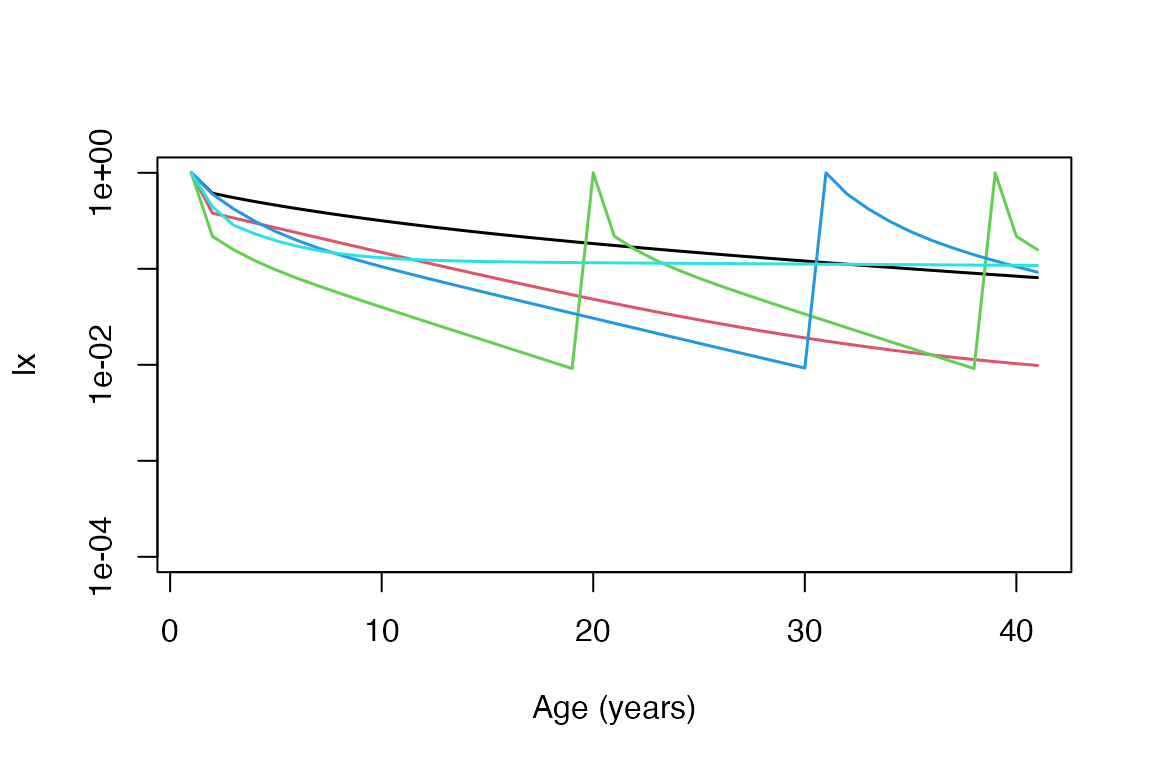
Now we’ll extend the basic approach above to many models. Specifically, we’ll examine trajectories of survivorship for all of the tree species in Compadre. Compadre is a database of matrix population models. You can read more about it here, and the associated R package here. The Rcompadre package contains a subset of the database that we can use to demonstrate computations on many models simultaneously.

First, we’ll subset Compadre to our group of interest (OrganismType == "Tree"). We’ll also remove matrices with missing values, and limit our selection to matrices with a periodicity (i.e. transition interval) of 1 year.

library(Rcompadre)
data(Compadre)

# In older versions of Com(p)adre the ProjectionInterval column was called
# AnnualPeriodicity.
if ("AnnualPeriodicity" %in% names(Compadre)) {
  Compadre$ProjectionInterval <- Compadre$AnnualPeriodicity
}

comp_flag <- cdb_flag(Compadre, "check_NA_U")

comp_use <- subset(comp_flag, OrganismType == "Tree" &
  check_NA_U == FALSE &
  ProjectionInterval == 1)

Let’s take a look at the species/populations that made the cut.

CompadreData(comp_use)[, c(
  "SpeciesAccepted", "MatrixPopulation",
  "MatrixTreatment"
)]
#> # A tibble: 7 × 3
#>   SpeciesAccepted          MatrixPopulation                      MatrixTreatment
#>   <chr>                    <chr>                                 <chr>          
#> 1 Phyllanthus indofischeri Biligiri Rangaswamy Temple Wildlife … Fruit harvesti…
#> 2 Phyllanthus indofischeri Biligiri Rangaswamy Temple Wildlife … Fruit harvesti…
#> 3 Castanea dentata         Leelanau                              Unmanipulated  
#> 4 Phyllanthus emblica      Biligiri Rangaswamy Temple Wildlife … Time since las…
#> 5 Phyllanthus indofischeri Biligiri Rangaswamy Temple Wildlife … Unmanipulated  
#> 6 Manilkara zapota         Central Veracruz state                Unmanipulated  
#> 7 Rhododendron ponticum    Ockham Common Nature Reserve          Unmanipulated

Notice that there are 3 matrices for the species Phyllanthus indofischeri, reflecting different treatment groups. Let’s collapse these replicates down to a single matrix per species, by averaging the relevant MPMs using cdb_collapse(). We’ll also use the function cdb_id_stages(), to make sure we’re only collapsing matrices that have the same stage class definitions.

# add column ID-ing matrices with same MatrixClassAuthor vector
comp_use$stage_id <- cdb_id_stages(comp_use)

# collapse database to single matrix per species * MatrixClassAuthor
comp_collapse <- cdb_collapse(comp_use, "stage_id")

# check species/populations again
CompadreData(comp_collapse)[, c(
  "SpeciesAccepted", "MatrixPopulation",
  "MatrixTreatment"
)]
#> # A tibble: 5 × 3
#>   SpeciesAccepted          MatrixPopulation                      MatrixTreatment
#>   <chr>                    <chr>                                 <chr>          
#> 1 Phyllanthus indofischeri Biligiri Rangaswamy Temple Wildlife … Fruit harvesti…
#> 2 Castanea dentata         Leelanau                              Unmanipulated  
#> 3 Phyllanthus emblica      Biligiri Rangaswamy Temple Wildlife … Time since las…
#> 4 Manilkara zapota         Central Veracruz state                Unmanipulated  
#> 5 Rhododendron ponticum    Ockham Common Nature Reserve          Unmanipulated

Next, let’s look at the organized stage classes for each MPM. If any of our MPMs include propagule or dormant stage classes, we may want to account for them when calculating lx.

MatrixClassOrganized(comp_collapse)
#> [[1]]
#> [1] "prop"   "active" "active" "active" "active" "active" "active"
#> 
#> [[2]]
#> [1] "active" "active" "active" "active" "active" "active" "active" "active"
#> 
#> [[3]]
#> [1] "active" "active" "active" "active" "active" "active"
#> 
#> [[4]]
#> [1] "active" "active" "active" "active" "active" "active" "active" "active"
#> [9] "active"
#> 
#> [[5]]
#> [1] "active" "active" "active" "active"

Indeed, 1 MPM includes a propagule stage. So let’s use the function mpm_first_active() to determine the first ‘active’ stage class for each MPM, which we’ll use to define the start of life.

comp_collapse$start_life <- mpm_first_active(comp_collapse)

Finally, we’ll use lapply() to apply the function mpm_to_lx to each row of comp_collapse. By default, lapply() will return a vector for each row, and the length of which is xmax. We can convert the output to an matrix, with columns representing each row from comp_collapse using do.call. After that, we’ll use the function matplot() to plot age-trajectories of survivorship for each species.

lx_list <- lapply(seq_len(nrow(comp_collapse)),
  function(x, comp_collapse) {
    U <- matU(comp_collapse$mat[[x]])

    rownames(U) <- colnames(U) # ensure row and col names are present

    mpm_to_lx(
      matU = U,
      start = comp_collapse$start_life[x],
      xmax = 40
    )
  },
  comp_collapse = comp_collapse
)

lx_array <- do.call(cbind, lx_list)
#> Warning in (function (..., deparse.level = 1) : number of rows of result is not
#> a multiple of vector length (arg 3)

matplot(lx_array,
  type = "l", lty = 1, log = "y", ylim = c(0.0001, 1),
  lwd = 1.5, xlab = "Age (years)", ylab = "lx"
)

References

Caswell, H. (2001). Matrix Population Models: Construction, Analysis, and Interpretation. 2nd edition. Sinauer Associates, Sunderland, MA. ISBN-10: 0878930965

Patrick Barks

2024-03-30

Introduction

Preliminaries

Age-from-stage methods with a single matrix population model

Extending to many matrix population models

References